What Is Time Complexity?
Time complexity, or Big O notation, is one way describing how the time it takes to execute your function grows as the size of the input increases. In other words, this is a simplified analysis of an algorithm’s efficiency; it is independent from the machine algorithms run on because it only focuses on basic computer steps.
If we say that the time complexity of an algorithm is \(O(n)\), where \(n\) is the size of the input, it represents that the time it takes to run it grows linearly with respect to \(n\).
Rules of Big O Notation
Drop the Constants
If you have a function whose algorithm requires \(2n\)-time steps, its time complexity is \(O(n)\), NOT \(O(2n)\). That is because as \(n\) gets larger, the coefficient \(2\) no longer matters.
Pick the Most Dominant Term
The time complexity of an algorithm which needs \((n^2+n)\)-time steps is \(O(n^2)\) because as \(n\) increases, we can ignore the impact of \(n\) compared to \(n^2\).
The dominance of each time complexity can be compared with others in the following order;
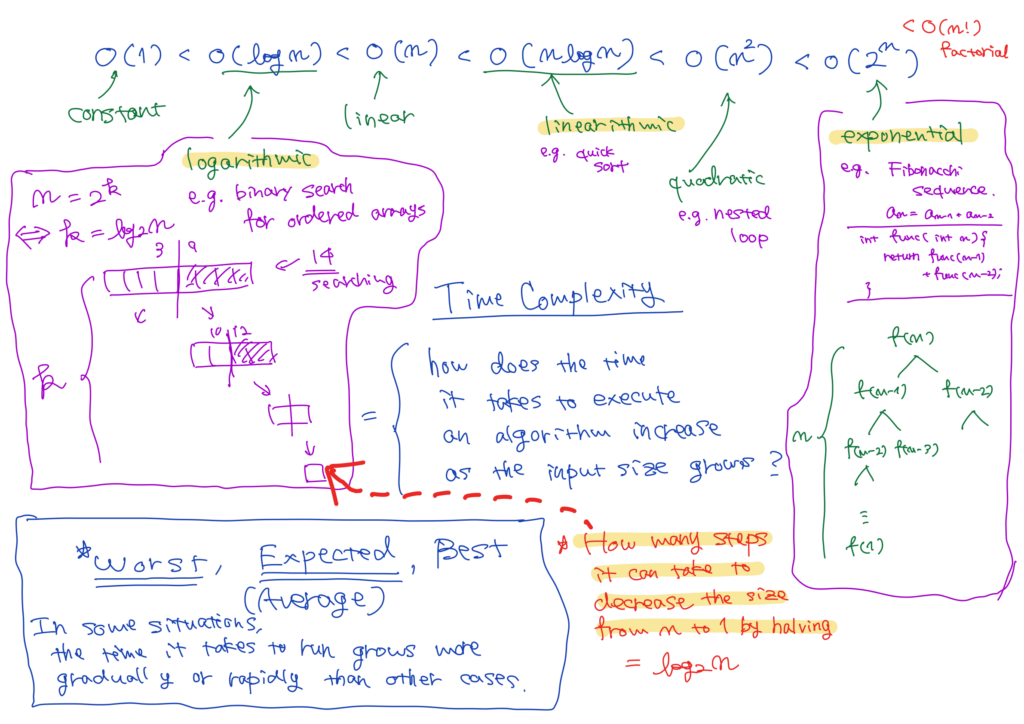
\(O(n!) > O(2^n) > O(n^2) > O(n \log n) > O(n) > O(\log n) > O(1).\)
The more you go to the left, the more dominant.
The Most Common Time Complexities
Logarithmic Time Complexity
Binary search, for instance, has logarithmic time complexity, \(O(\log n).\) In this algorithm, we look for one element, \(x\), in an \(n\)-element sorted array in the following way;
- Compare \(x\) with the midpoint of the array, \(m\).
- If \(x\) equals \(m\), we return. If \(x\) is greater than \(m\), we search on the right side of the array. If \(x\) is less than \(m\), we search on the left side of the array.
- We stop the following operations when we find \(x\), or when the size of the array reaches one.
In other words, unless we find the value, the size of the array halves with each attempt. Therefore, the runtime is how many steps it can take to decrease the size from \(n\) to \(1\) by halving. That is what \(\log_{2}n\) means exactly.
(Note: While binary search for a sorted array has logarithmic time complexity, the same principle does not necessarily apply to a tree data structure. The search operation in a binary search tree could have a worse time complexity, possibly linear; in the case where the tree is NOT balanced.)
Exponential Time Complexity
A function which calls two recursive functions has exponential time complexity, \(O(2^n)\); a well-known example is a function that calculates \(n\)-th element in a Fibonacci sequence with an input of \(n\), where the two previous recursive functions are called with inputs of \(n-1\) and \(n-2\).
The Best, Worst and Expected Case
The time complexity of a specific algorithm could vary due to its input or scenario. It means that for some specific inputs or scenarios, as the input size increases, the time required to execute the function grows more rapidly or gradually than in other cases.
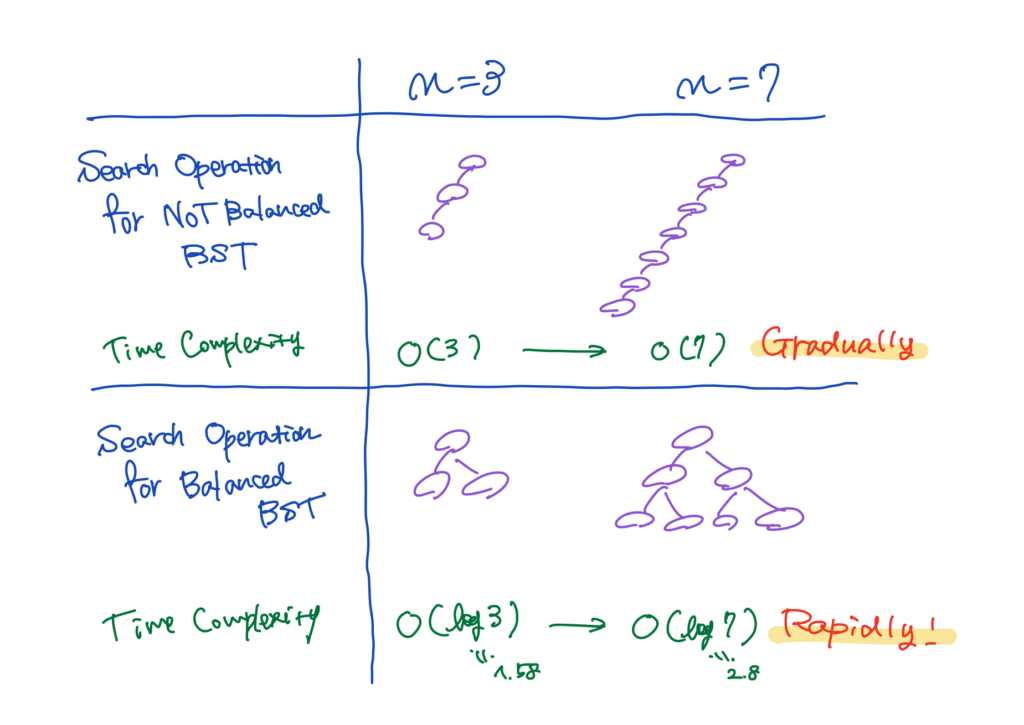
We can actually describe time complexities in three different ways; the best case, the worst case and the expected case (or average case). Usually, the worst case and the expected case are discussed to evaluate the efficiency of an algorithm.
Amortized Time Complexity
Amortized time complexity is a way describing the algorithms where the worst case happens every once in a while, but once it happens, it won’t happen again for a long time. It enables us to evaluate the efficiency of algorithms over a sequence of operations rather than just a single trial.
For instance, ArrayList, or dynamically resizing array is implemented so that when it reaches its capacity, it doubles its size. This operation encompasses creating a new array, and copying every element in the previous array into new one. The worst cases are when an ArrayList reaches its capacity, but they rarely happen. Therefore, ArrayList insertion efficiency should be analyzed using the concept of amortized time complexity for \(n\)-time insertions.
If an ArrayList starts with \(1\), when it reaches the capacity, its size will be \(1, 2, 4, 8, …, n\). Because each insertion takes \(1, 2, 4, 8, …, n\) steps, where \(n\) is a power of \(2\), \(n\)-time insertions take \(2n\) steps;
\(1 + 2 + 4 + … + n = n + \frac{n}{2} + \frac{n}{4} + … + 1 = 2n.\)
Therefor, the amortized time complexity for each insertion is \(O(1) = O(2n)/n.\)
Reference
- Gayle Laakmann McDowell. (2015). Cracking the Coding Interview: 189 Programming Questions and Solutions (6th ed.). CareerCup.
- (What is time complexity?)
- (Intuitive explanation on the concept of amortized time complexity) https://medium.com/@satorusasozaki/amortized-time-in-the-time-complexity-of-an-algorithm-6dd9a5d38045
