Trees
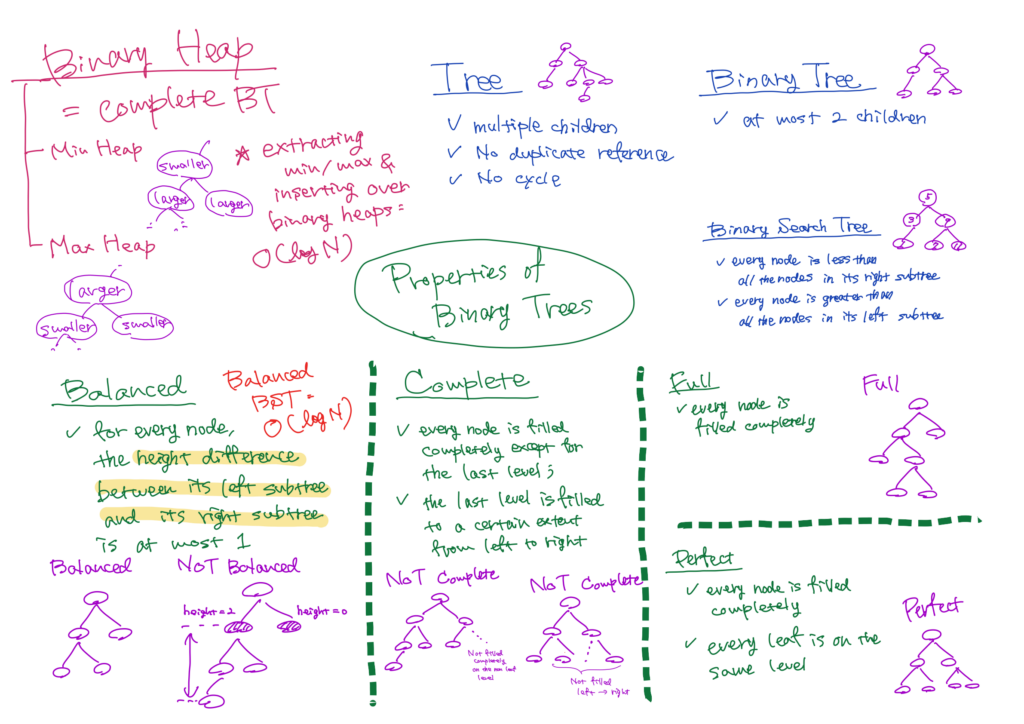
What Is a Tree?
A tree is a data structure similar to a linked list. While in a linked list, each node can link to only one other node, in a tree, each node can link to multiple other nodes, which are called child nodes or just children.
Additionally, a tree must satisfy the following conditions:
- There are no two references which point to the same node; duplicate references are not allowed.
- There are no cycles.
In other words, there must be exactly one possible path from the root to reach every other node.
Binary Trees and Binary Search Trees
If in a tree, every node has at most two children, it is called a binary tree. Particularly, binary trees which satisfy the following conditions are called binary search trees.
- Each node is greater than every node in its left subtree.
- Each node is less than every node in its right subtree.
Balanced Trees
A binary tree is balanced, if the height difference between the left subtree and the right subtree is at most \(1\) for every node.
In terms of efficiency, being balanced is preferred. For instance, balanced binary search trees enable us to execute the main operations such as find, insert and delete over them with logarithmic time complexity. This is consistent with the fact that logarithms indicate how many steps it can take to reduce the size from \(n\), the number of nodes, to \(1\) by halving, which exactly corresponds to the height of balanced trees.
Complete, Full and Perfect Binary Trees
A binary tree is classified as a complete binary tree when every non-leaf node is filled completely except the last level, and the nodes on the last level are filled from left to right.
Additionally, when every non-leaf node has two children, the binary tree is referred to as a full binary tree.
Furthermore, if every non-leaf node has two children, and every leaf is on the same level, we call it as a perfect binary tree.
Binary Heaps
What Is a Binary Heap?
A binary heap is identical to a complete binary tree. Specifically, binary heaps in which every node’s value is less than or equal to that of its parent are called max-heaps. On the other hand, if every node’s value is greater than or equal to that of its parent, they are min-heaps.
Operations
Min-heaps (max-heaps) enable us to execute the operations of insertion and extracting the minimum (maximum) node with logarithmic time complexity.
When inserting, a min-heap (max-heap) works in the following way.
- Insert a new node at the bottommost and rightmost spot.
- If the new node is less (greater) than its parent, swap them.
- Repeat this operation until it satisfies the condition of min-heaps (max-heaps).
As for extracting the minimum (maximum) node, we start with extracting the root. Afterward, we follow these steps:
- Place the bottommost and rightmost node at the root.
- If the new node is greater (less) than both of its children, swap the new node with the smaller (larger) of its two children.
- Repeat this operation until it satisfies the condition of min-heaps (max-heaps).
These algorithms take \(O(\log n)\) time because they involve bubbling up or down a node through the height of a balanced binary tree.
Graphs
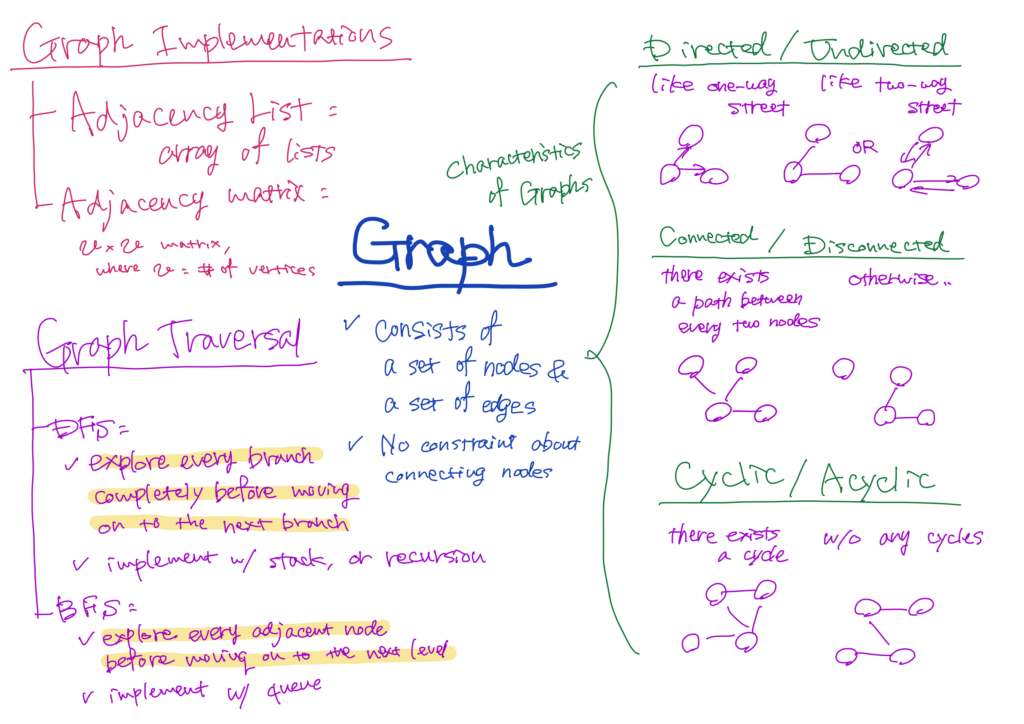
What Is a Graph?
A graph is a data structure which consists of a set of nodes and a set of edges. Unlike a tree, in a graph, there is not any constraint about connecting nodes. Graphs are specified with respect to the following aspects.
- Directed or undirected: whereas directed edges are like a one-way street, undirected ones are like a two-way street.
- Connected or disconnected: a graph is connected if there is a path between every two node.
On the other hand, a graph which consists of some isolated subgraphs is disconnected. - Cyclic or acyclic: a graph is acyclic if it does not contain any cycles.
Otherwise, it is called cyclic.
Technically, a tree is a connected and acyclic graph.
Graph Implementations
We are going to discuss the common ways to represent graphs; adjacency list and adjacency matrix.
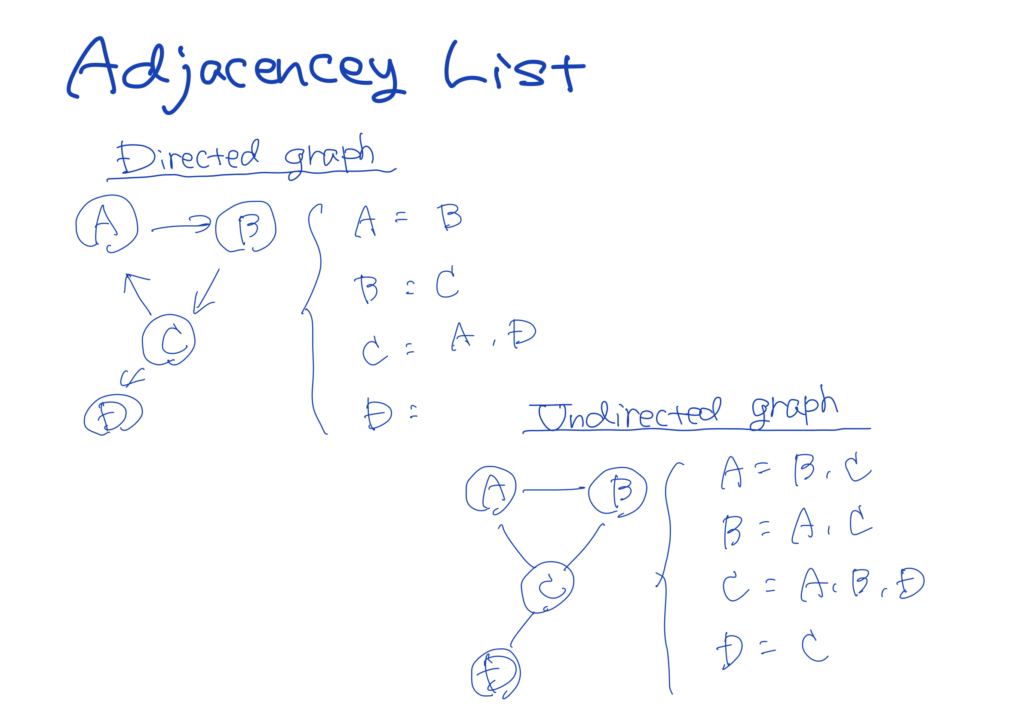
When implementing a graph with an adjacency list, every vertex possesses a list of adjacent vertices. In other words, an array (or a hash tables) of lists (arrays, linked lists, etc.) can be usd to represent a graph.
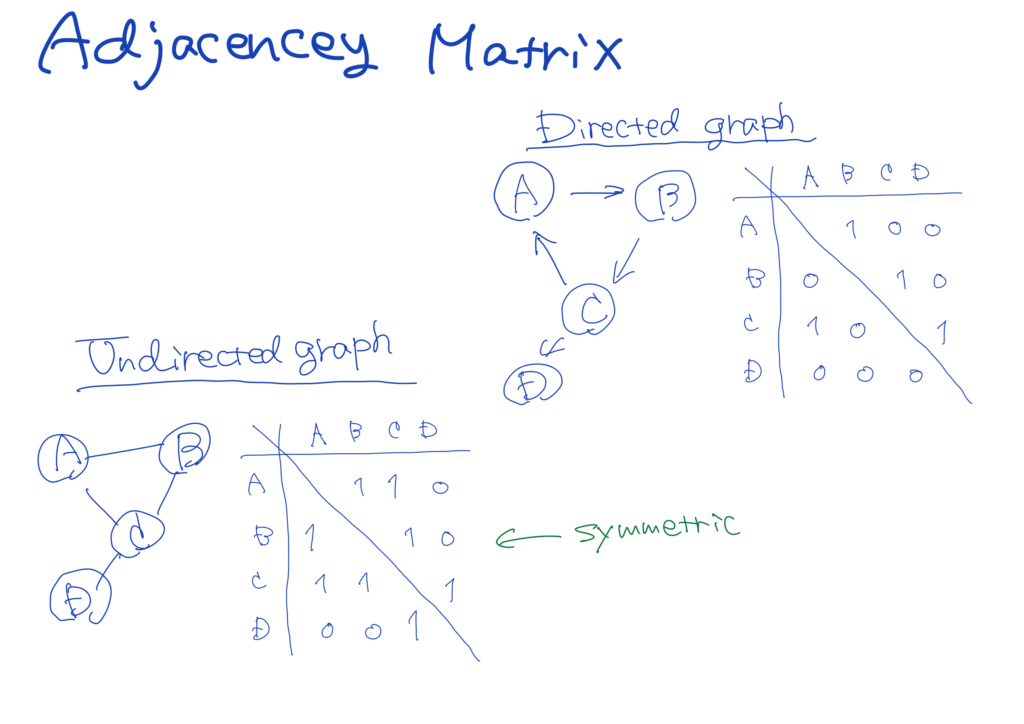
As for adjacency matrices, we use a \(v \times v\) boolean matrix, where \(v\) is the number of nodes. The value of matrix[i][j] is true if there is an edge from node \(i\) to node \(j.\)
Graph Traversal
There are two common ways to traverse graphs; depth-first search and breadth-first search.
In depth-first search, or DFS, we start at the root and explore every branch completely before moving on to the next branch. DFS is equivalent to the concept of backtracking.
On the other hand, in breadth-first search, or BFS, we start at the root and explore every adjacent node before moving on to the next level. BFS is preferred when finding the shortest path between two nodes.
While a last-in-first-out (LIFO) stack, or recursion, is used to implement DFS, BFS employs a first-in-first-out (FIFO) queue for traversal.
The time complexity for both DFS and BFS is \(O(V+E)\) where \(V\) and \(E\) represent the numbers of vertices and edges.
This is because, firstly, visiting every vertex takes constant time respectively, so \(O(V)\) in total. Secondly, if we implement the graph using an adjacent list, for each vertex \(i\), we traverse its adjacent vertices, which takes \(O(E_i)\) respectively, and \(O(E)\) in total. Here, \(E_i\) represents the number of adjacent vertices of vertex \(i\), therefore, \(E = E_1 + E_2 + … + E_n .\) Consequently, the time complexity is \(O(V+E) .\)
However, when using an adjacency matrix, for each vertex, the number of vertices we’re going to traverse is \(V\) respectively. Therefore, traversing takes \(O(V^2)\) in total, and the overall time complexity becomes \(O(V+V^2) = O(V^2) .\)
Traversing a tree without any duplicate references takes \(O(V)\) time, because in this case the total number of edges equals one less than the number of vertices.
Reference
- Introduction to the data structures:
- Gayle Laakmann McDowell. (2015). Cracking the Coding Interview: 189 Programming Questions and Solutions (6th ed.). CareerCup.
- (Trees) https://youtu.be/1-l_UOFi1Xw?si=J1Ll9OZinzp9HwEi
- (Binary heaps) https://youtu.be/0wPlzMU-k00?si=xV-GO9S1752-kLvE
- (Graphs) https://youtu.be/gXgEDyodOJU?si=ZOKdsWy-tNnpgk15
- Confusing terminologies regarding the completeness of binary trees:
- Intuitive explanations on graph traversals:
- Why is the time complexity of DFS and BFS O(V+E)?:
