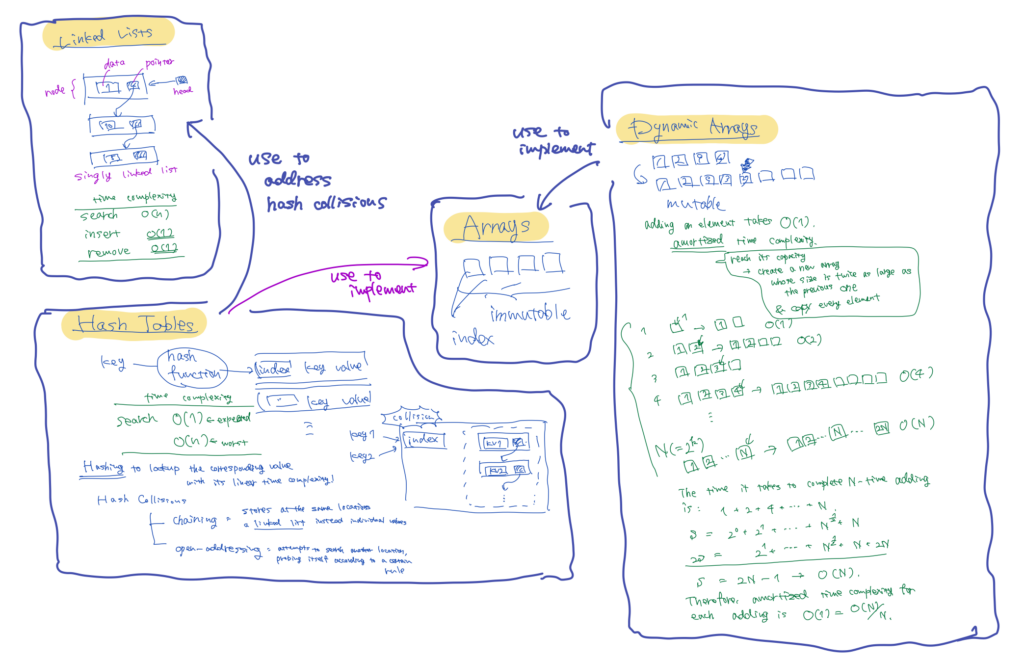
Linked Lists
What Is Linked List?
A linked list is a data structure that stores elements, or nodes, in a linear order. Nodes in a linked list, have both data and only one pointer to the next node. They are called as singly linked lists. In some linked lists, nodes also have another pointer to the previous one; doubly linked lists. In other words, in linked lists, pointers determine the ordering.
Linked lists have the special pointer. The pointer which points to the first node is called as head. Some of them also have another special pointer which points to the last node; tail.
Operations
We are going to discuss about how the main operations work with linked lists; search, insert and delete.
First, in a search operation, we iterate through a linked list from the head to the tail unless we find the value. Therefore, its time complexity is \(O(n)\), where \(n\) is the size of the linked list.
The next one is to insert a new node at the beginning of a linked list. It encompasses the three steps:
- Set the new node’s next pointer equal to the original head, which refers to the original first node.
- Only if the list is doubly linked, set the original first node’s previous pointer equal to the new node.
- Set the head pointer to the new node.
Obviously, these steps have a constant time complexity, \(O(1)\), because the time it takes to insert does not change as the size of the linked list increases.
Then, to delete an existing node at the beginning of a linked list works in the similar way, and its runtime is also \(O(1)\).
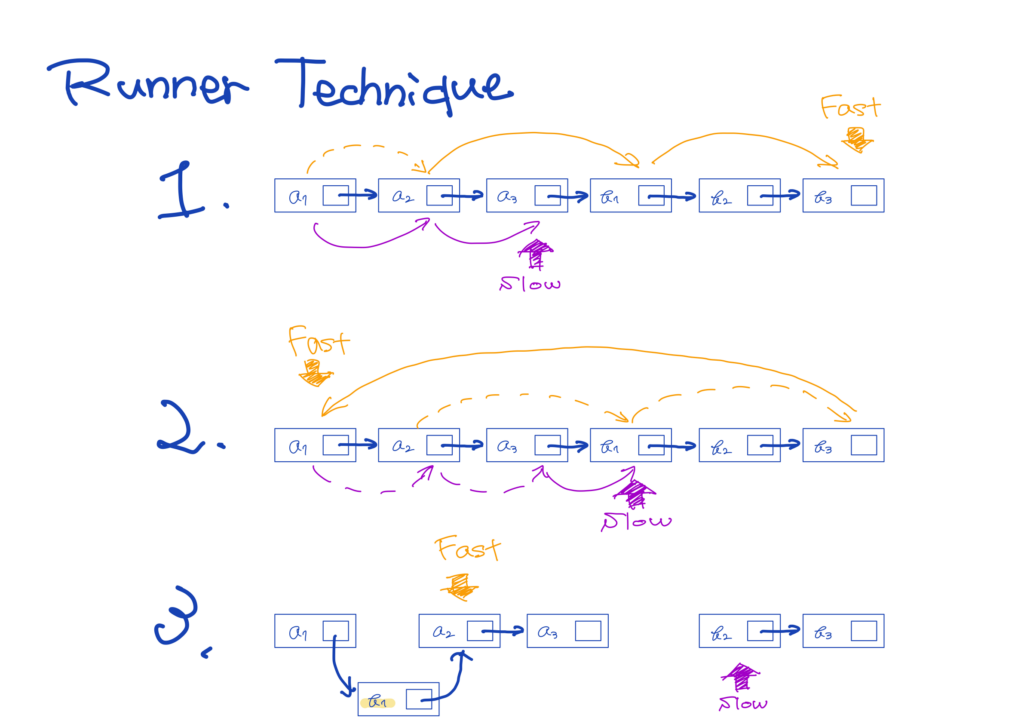
Runner Technique
In the runner technique, we iterate through a linked list with two iterators simultaneously, with one ahead of the other. For instance, the fast iterator is ahead of the slow one by a fixed distance. In other cases, the fast iterator hops multiple nodes for every step the slow one makes.
The latter technique can be used to detect cycles in a linked lists. Additionally, it would be helpful to solve the following problem:
- We have a linked list: \(a_1, a_2, …, a_n, b_1, b_2, …, b_n\). Our goal is to rearrange it as follows: \(a_1, b_1, a_2, b_2, .., a_n, b_n\).
- We don’t know its length, but know that it’s even.
- We can only manipulate the order of the original linked list; we can’t use any additional linked lists.
First, we need to make sure that one iterator is at the midpoint of the linked list. In this case, let the fast iterator start at the next node to the head, and let the slow one start at the head. Moreover, the fast iterator only touches two other nodes, while slow one goes through all the nodes. When the fast reaches the last node, the slow is located precisely at the midpoint.
Next, let the fast iterator move to the head of the linked list, and let the slow one advance by one node. Now, we have the list in which the fast is at the beginning (\(a_1\)), and the slow is at the midpoint (\(b_1\)).
Then, iterate through it with two iterators simultaneously using the following approach.
- The fast iterator selects the node.
- The slow one picks the node and places it immediately after the previous node the fast one picked.
- The fast advances through two other nodes.
- The slow advances through one node.
- Repeat this operations until the slow iterator reaches the end.

Hash Tables
What Is Hash Table?
A hash table is a data structure that maps keys to values.
A simple hash table can be implemented using an array and a hash function. What hashing does is attempt to associate a given key with an index which refers to the location where the corresponding value is stored. This means that in order to retrieve a value, a hash table just calculates an index using its hash function with the input of an index.
This is why the strength of hash tables lies in efficient search operations; they allow us to find the corresponding value for a key in \(O(1)\) time on average, or \(O(n)\) in the worst case.
How To Address Hash Collisions
A hash function can return the same value for two different inputs, which is known as hash collisions. To address hash collisions, there are two most well-known techniques: chaining and open-addressing
In chaining, when a hash tables faces a hash collision, it stores a linked list at the location, instead of a single key-value pair. This linked list contains the key-value pairs whose hashed indices are identical.
On the other hand, in open-addressing, if the location where a value is supposed to be stored is already occupied, a hash table attempts to search another vacant location to store the value, probing itself according to a certain rule.
Resizable Arrays
What Is Resizable Array
An array is a data structure used to store elements, whose indices allow us to retrieve elements easily. The simplest form is a static array, whose size cannot be modified. Therefore, when you add an element beyond the size of an array, a new array which has enough vacancy is created, and all the elements are copied to it. On the other hand, a resizable array, or dynamic array can change its capacity as needed.
Operations
Adding a new element to a resizable array, only when it reaches its capacity, involves creating a new array whose capacity is twice as large as the previous one, and copying all the elements. Since the worst scenario rarely happens, the time efficiency of this operation is typically evaluated using amortized time complexity, which is \(O(1)\).
Other Data Structures
StringBuilder in Java
Let’s discuss about the operation of concatenating multiple strings; how to implement it, and how to execute it more efficiently.
Suppose that we have an \(n\)-size array of strings, and each length is \(a_1\), \(a_2\), …, \(a_n.\) If the operation is implemented in the following way, in each iteration of the loop, a new copy of the string is created, and the two strings are copied over, character by character.
String concatenate(String[] words){
String sentence = "";
for(String word : words){
sentence = sentence + word;
}
return sentence;
}Consequently, the number of steps this function requires is \(a_1 + (a_1+a_2) + … + (a_1+a_2+…+a_n)\). For simplicity, if \(a_i\) equals \(a\) for every \(i=1,2,…,n\), this becomes
\(a + 2a + … + na = a(1+2+…+n) = \frac{1}{2}an(n+1)\).
It means that the function has a quadratic time complexity, \(O(n^2)\).
On the other hand, this operation works more efficiently when using StringBuilder, because it does not create any copies of the string in each iteration of the loop.
String concatenate(String[] words){
StringBuilder sb = new StringBuilder();
for(String word : words){
sb.append(word);
}
return sb.toString();
}Since the capacity of a StringBuilder object expands automatically as needed, the amortized time complexity for \(n\) appending trials is \(O(n)\). Additionally, toString has a runtime of \(O(an)\). Consequently, the latter function has a linear time complexity, \(O(n)\).
Reference
- Gayle Laakmann McDowell. (2015). Cracking the Coding Interview: 189 Programming Questions and Solutions (6th ed.). CareerCup.
- (Linked lists)
- (What are linked lists?) https://youtu.be/F8AbOfQwl1c?si=NLFJFM_0n_Gj-uWd
- (Operations and time complexities of linked lists) https://youtu.be/Ovhj6qDSF9M?si=jfqbzDmFLxWq0mUJ
- (Runner technique: detect a cycle of linked lists) https://youtu.be/MFOAbpfrJ8g?si=PWC84ljE3MRx9IK-
- (Runner technique: rearrange linked lists) https://stackoverflow.com/a/30546453
- (Hash tables)
- (What are hash tables?) https://youtu.be/knV86FlSXJ8?si=AZ1kNThUUHRIH-5p
- (Hash Collisions) https://youtu.be/kNheXzNOcm4?si=6YucMRU4XdhQEAk1
- (Resizable arrays)
- (What are static arrays and dynamic arrays?) https://youtu.be/qTb1sZX74K0?si=UA6QjHh1ky48Wd3n
